Introduction:
The measurement of the rate at which oxygen is consumed can provide valuable information as it pertains to assessing levels of cardiorespiratory fitness, estimating calories burned during activity, and estimating physiological mechanisms related to metabolic function such as proper dosing of drug medications. There are inherent difficulties associated with the accurate determination of aerobic power. The most salient of these difficulties is the cost of indirect calorimetry equipment. As a result, professionals practicing in the field of exercise physiology find it valuable to predict aerobic power through the utilization of maximal and submaximal graded exercise tests.
Although these tests are easy to perform, and inexpensive in comparison to respiratory gas analysis, there are a number of key factors involved in the accurate estimation of oxygen uptake that are not currently in practice. The purpose of this paper is to identify a standardized method to increase the accuracy of the predictive equations that are currently in use. These equations include those used in submaximal treadmill and bicycle testing, metabolic equations published by the American College of Sports Medicine, protocols used by the YMCA, and the multitude of protocols and MET calculations that are in existence in exercise facilities, Universities, and rehabilitation facilities throughout the world.
Effect of Heart Rate
A number of testing protocols that have attempted to estimate aerobic power based on the heart rate response to submaximal workloads. By extrapolating the slope of the heart rate/workload relationship to a maximal heart rate, maximal aerobic power can be estimated. The greatest error in predicting maximum aerobic power appeared to be in the estimation of maximal heart rate, with errors as high as 10-20% when extrapolating submaximal data. (McArdle, 1981)
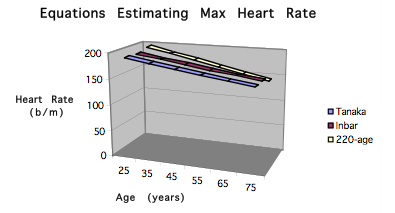
By far the most widely used equation for the estimation of maximum heart rate has been credited to Karvonen: HRmax= 220-age. Credit for its creation was denied by Karvonen, and appears to have been a mere observation by Fox (1971) concerning maximum heart rates in a group of subjects in a published study. An excellent history of the HRmax=220-age equation, can be found in a paper by Robergs and Ladwehr (2002). Currently, the estimation of maximum heart rate by Tanaka (2001) appears to have the highest correlation of actual measurements to maximum heart rate, (r=0.81) for both men and women, but did not report a standard error of estimate. In their review, Robergs and Landwehr analyzed the data and created a regression equation from 30 studies estimating heart rate and found that it closely matched the equation of Tanaka.
Since the Standard Error of Estimate for estimating maximum heart rate is still unacceptably high, the ability to use actual maximum heart rate is the preferred method when available. For safety reasons this may not be possible, so the Tanaka equation based on age may be the best equation to estimate maximum heart rate that is available to date.
Figure 1: Similar results are noted in the equations by Tanaka and Robergs, while the 220-age equation tends to underestimated maximal heart rates of older subjects.
Another factor to consider, is the selection of acceptable workloads during submaximal graded exercise testing. Submaximal aerobic testing extrapolates the slope of the heart rate/ workload relationship, to an estimated maximum workload, heart rate and oxygen uptake. This method asserts that the stroke volume remains stable throughout the extrapolated slope of the heart rate/work load relationship. It has been noted that the stroke volume reaches near maximum at 40-60% of Max VO2, (Astrand, 1977) and remains relatively stable between 40 to 80% of maximal VO2, (Ross, 1989). This appears to be fairly consistent even among congestive heart failure patients, who reach maximum stroke volumes at 55% of Max VO2 and beyond (Massey, 2001). Therefore, the slope of the heart rate workload relationship used to estimate Max VO2, should attain a minimum of 40%, and a maximum of 80% of Max VO2, to ensure that the linear increase in heart rate is directly representative of the increase in workload.
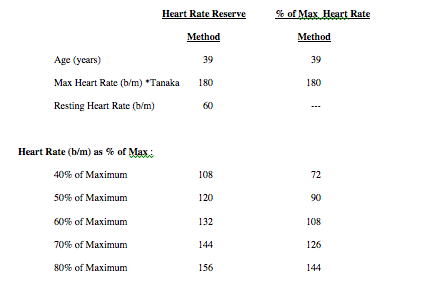
Lastly, exercise physiology should standardize the Heart Rate Reserve Method in calculations of percent of maximum estimates. The Heart rate Reserve Method, ironically derived by Karvonen (1957), calculates the difference between the resting heart rate and the maximum heart rate and refers to this as the heart rate reserve. A comparison of the differences between the Heart Rate Reserve Method and the Percent of Max Heart Rate Method are presented below utilizing the equation of Tanaka to estimate maximum heart rate, (Table 1).
Table 1: Comparison of Karvonen’s Heart Rate Reserve Method, versus the % of Max Heart Rate Method in determining various exercise intensities.
The American College of Sports Medicine early guidelines utilizing the Heart Rate Reserve Method, suggested 60-90% of maximum heart rate as equivalent to 50-85% of maximum VO2, (1983). This was in contrast to Burke (2001), and Heyward (1997) who stated the Heart Rate Reserve Method has a nearly direct correlation to percent VO2. Burke inferred the correlation of heart rate and VO2 proposed by the ACSM was more in line with research using % Max Heart Rate rather that % Heart Rate Reserve Method. Later versions of the ACSM guidelines (1991) recommended 40% to 85% of heart rate reserve as an exercise intensity for general aerobic fitness training. These recommendations may be considered overly conservative in light of advancements in the training and availability of fitness professionals, and in technological advances found in heart rate monitoring devices.
To summarize the use of heart rate for the estimation of oxygen consumption:
- Do not rely on the 220-age formula, others are available with better accuracy, Tanaka (2001): 207-(age * .7), or Inbar (1994): 205.8-(age * .685) (1994).
- If the extrapolation of the slope of a heart rate/workload relationship is the method employed to predict maximal oxygen uptake, ensure that the range used is between 40% to 80% of Heart Rate Reserve.
- Universal agreement of the Heart Rate Reserve Method versus the Percent of Maximum Heart Rate Method when referring to percentage of heart rate intensity.
Oxygen Uptake and Metabolism at Rest
Most information derived from the measurement of oxygen uptake during exercise is collected using indirect calorimetry. Investigators generally recognize resting oxygen uptake as equal to 3.5 ml of oxygen consumed per kilogram per minute (ml/kg*min “1). By measuring oxygen uptake in ml/kg*min “1 during activity, investigators believed that they could determine the oxygen needed to perform various activities. The beauty of the model was that different sized individuals would possibly require the same relative oxygen uptake on a per weight basis.
Measurements of oxygen uptake during various physical activities were assigned a relative value, regardless of the individual’s body weight as were using weight and not height or other variable. A subject of twice the mass would require twice the oxygen of their half-sized contemporary during a similar activity. Consequently, the larger individual would be able to perform twice the absolute work at the same relative oxygen uptake.
Theoretical Model Showing Relationship of Workload, and Oxygen Uptake as it Relates to Body Mass
Effects of Body Dimension
But does a subject of twice the weight have twice the blood volume, or lung capacity of a person half their body weight? Early work by Hill (1950) found that work,(i.e. force and power) are two dimensional or squared quantities, while mass and volume measurements are three dimensional or cubed quantities. Thus by adopting a 2/3 exponent, into the units of measurement, investigators could incorporate these known physical laws. Hill postulated that relative strength and endurance is related more to the mass of the subject raised to a 2/3 exponent.
M. H. Lietke (1956), used this very formula in predicting relative strength of world record weightlifting performances. With the weight lifted plotted against the mass of the lifter raised to the 2/3 power, performances could be evaluated across weight classes. This later evolved into the creation of the Hoffman Formula (O’Shea, p. 185). Using this method, the best single performance to date is that of Galabin Boevski of Bulgaria in the 69 kilogram weight class, lifting a combined total of 357.5 kilos. (Figure 3)

Figure 3: Predicted strength to weight ratios (mass to the power of 2/3), compared to actual strength to weight ratios for current world record Olympic weightlifters by weight class. (International Weightlifting Federation Web Page).
Renowned exercise physiologist, Per-Olof Astrand, was first to note the impact of mass and body dimensions on the assessment of maximal oxygen uptake for individuals. Astrand stated that ‘maximal oxygen uptake, expressed as ml * min “1 * kg “2/3, is not related to body weight, and may therefore be used as a meaningful fitness index instead of conventional methods of expressing maximal oxygen uptake as ml * kg “1, which penalizes heavy individuals. (1977, p. 377).
This was consistent with the research of McMahon and Bonner (1983), examining the relationship of body mass to oxygen consumption in guinea pigs. O. Vaage and Hermansen (1977) found that in similarly trained elite athletes, the deviation from a perfect 2/3 predictive relationship between mass and oxygen uptake, was 0.86 when plotted against liters of oxygen uptake per minute, (bigger athletes had higher absolute consumption), the deviation was -.69 when plotted against ml/kg*min-1 (smaller athletes had higher relative consumption) and “.06 when plotted against ml/kg^-2/3*min-1. Athletes, regardless of size, did not deviate far from the predicted 2/3 relationship.
Mass as it Relates to Basal Metabolic Rate
Research conducted by Kleiber (1932), showed that for mammals of different body dimensions, basal metabolic rate held a consistent scaling to the power of 3/4, rather than a 2/3 exponent when analyzed across the range of dimensions from a mouse to an elephant. Kleiber originally postulated that the 3/4 relationship for basal metabolism was valid across a variety of species, but within the species it may be closer to 2/3. But McMahon & Bonner (p. 66), noted in species that have larger variances of body mass such as dogs, that ‘there individual species slope is close to .75.
Instead of relating the mass to force or power as in when the animal is engaged in activity, Kleiber’s Law found consistency with the theory of elastic similarity. The theory of elastic similarity simply stated ‘predicts that the cross-sectional area of any anatomical feature of the body is proportional to mass 3/4 (McMahon & Bonner, p. 130). So the cross sectional area of the body segments in proportion to mass may be the determining factor in estimating basal metabolism. Brody (1945), verified the experiments of Kleiber, finding a similar relationship raised to the .74 power. Kleiber’s equation to estimate basal metabolic rate in humans is still in use today by the manufacturers of indirect calorimetry equipment, (Sensormedics, p. 15-4).
The information provided by Kleiber and Astrand infers the relationship between mass and oxygen uptake may change from a slope of 3/4 in basal conditions to a 2/3 slope at maximal oxygen uptake. This appears to make intuitive sense. When in a resting state, the volume of the skeletal voluntary muscle mass is dormant, while the autonomic system, is always metabolically active. As exercise intensities increase, blood may be shunted away from the organs and smooth muscles into the more dynamic and active working muscles. The basal metabolic contribution to the total oxygen uptake is altered, thus reflecting the noted change seen in its relationship to body mass. This could explain the shift of the slope from 3/4, in basal conditions as proposed by Brody and Kleiber, to the 2/3 proposed by Vaage & Hermansen, and Astrand during maximal aerobic exercise.
Body Surface Area as it Relates to Metabolic Rate
Another factor involved in the limitation of peak exercise performance and oxygen uptake is the dissipation of heat. This was first noted by the German physiologist Max Rubner (1883) who suggested that metabolic rate was somehow limited by the body’s surface area. It was Hemmingsen (1960) that actually plotted mass with body surface area and found slopes of .63 in elastically similar animals. Thus during maximal aerobic exercise their may be less oxygen consumed and less work being done because of an inability to radiate heat as effectively in larger animals. This would not be apparent in activities such as Olympic weight lifting, since there is no limitation by dissipation of heat in the performance of a single lift.
The widespread use of a relative resting MET of 3.5 ml/kg/min-1 for everyone makes no allowance for differences in body dimension in metabolic studies. This practice has no basis in fact, and can greatly affect the accuracy in which estimations of oxygen uptake are currently being made. Also the relationship between oxygen uptake and body mass does not appear to be a fixed 2/3 exponential relationship, but allometric, in that there could be changes in the relationship of mass to oxygen uptake depending on the intensity and type of exercise.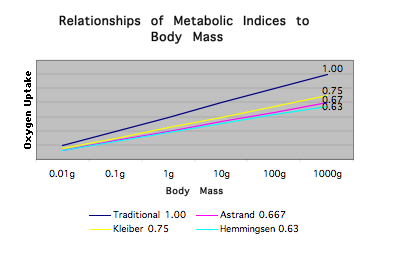
Figure 3: The effect of mass on variables related to oxygen uptake. (Traditional slope) = 1.0, Astrand, and Vaage & Hermansen slope for Max VO2 = .667, Kleibner slope for basal metabolic rate = .75, , Hemmingsen slope for body surface area = .63
Application of the Information
It is clear there are limitations of using measurements of oxygen uptake that are not adjusted for the mass of the subject. At the same time it may be impractical for physiologists in the future to have to review each study and adjust the metabolic values based on the weights recorded for the subjects analyzed. A workable solution to this dilemma must fulfill three requirements:
- A standardized method of measuring oxygen uptake and metabolism must be created.
- The equation, constant or conversion factor cannot be mathematically unwieldy.
- It must be able to correct the data that has been collected thus far.
Standardization of Measurement
One obvious solution in creating a method to standardize the measurement of oxygen uptake is to measure all aerobic scores in the units of milliliters of oxygen consumed per kilogram raised to the 2/3 power per minute, (ml*min-1*kg-2/3). In so doing, we have already broken our second requirement to create a system of measurement that is not too mathematically unwieldy to be practical. And the fact that the oxygen consumption may not be a linear 2/3 exponential relationship across various work intensities may make this solution too simplified.
Another option would be to standardize oxygen uptake measurements to the mass of a reference ‘averaged sized human. If a standard human mass is referenced, then all data from metabolic studies and parameters can be compared directly to one another. A total of 1800 active men and women, aged 18-90, achieve an average, reference weight for a human of approximately 75 kilograms (Surina, 2003). If 75 kilograms is the choice for a reference human, then all metabolic data will be in terms of what value would have been attained if the subject was of average mass.
The next step is to make a correction factor that can adjust metabolic data of subjects of varied mass, with our reference human. If this can be done effectively, then previous units used for the measurement of oxygen uptake are still valid, and can be adjusted by a correction factor. The preferred units of oxygen uptake could thus remain the MET, (metabolic equivalents), and the corrective adjustment of METs to the reference human would be termed a ‘Compensated MET. This effectively satisfies the first requirement, the creation of a method to standardize metabolic parameters and processes.
Creation of an equation that is not mathematically unwieldy
Dealing with a fractional exponent like 2/3 would require the use of a scientific calculator, (yx function). However, the ideal constant should involve a mathematical operation that can be done on a standard calculator.
If we go back to our original notion of a conversion factor that when multiplied to an existing measurement, we can obtain a ‘compensated value, we may be able to simplify the math. By creating a correction factor, we can work backwards to re-create the 1.00 slope that represents our reference human, (the reference human of 75 kg is not compensated for). Since a correction factor represents the difference between the 2/3 power and a 1.00 power of our reference human, a 1/3 exponent is created. By utilizing the reference human, the correction factor to obtain a 1.00 slope for our 75 kg model is:
Simple Compensated MET Formula:
Wt(kg)1/3 4.22
What the numerator in the Compensated MET formula implies is: what * what * what = wt(kg). Since 4.22 * 4.22 * 4.22 = 75 kilograms and 4.22 divided by 4.22 = 1.00, the metabolic data collected on a subject of 75 kilograms must be multiplied by a correction factor of 1.00 to obtain a ‘Compensated MET. Thus, the data remains unchanged. A subject of 125 kg with a cube root of 5, (5 x 5 x 5=125 kg), and 5 divided by 4.22 = 1.18 correction factor. All relative metabolic data collected on this subject would need to be multiplied by 1.18 to obtain the oxygen uptake score that an averaged size individual would have attained.
Since the cube root of an individual’s mass will seldom exceed a range of 3.5 to 5, it is merely a matter of trial and error on a standard calculator to find the cube root of a subject’s mass, or have a computer program that can make the calculation. This Compensated MET formula may be acceptable for the prediction of maximum oxygen uptake according to the data of Astrand, Vaage & Hermansen and McMahon and Bonner, and ideal for assessing relative strength, and power measurements consistent with the work of M.H. Lietke.
What about a formula for predicting metabolic rates, that incorporates the earlier data of Kleiber or Rubner or Hemmingsen? This unfortunately cannot be done easily with a simple calculator. The incorporaton of Klieber’s data says that in the basal condition, the slope of mass to oxygen uptake is 3/4. To make a correction factor like we did for our 2/3 exponent, 1.00 “ 0.75 (Klieber’s slope of 3/4) = 0.25. The 0.25 (or 1/4 power) exponent represents the basal conditions when the % of Heart Rate Reserve is equal to 0, and the subject is at their true resting heart rate and basal state.
At the other end of the metabolic continuum (VO2 max), the slope may more closely follow the slope of Hermingsen’s power of 0.63. A correction factor to achieve 100% of max oxygen uptake would have a slope of 0.37, (1.00 minus .63). If 0.25 represents the basal condition, (0% of Heart Rate Reserve), and 0.37 represents the maximum oxygen uptake, (100% of Heart Rate Reserve), then the exponential span covers 0.37-0.25 = 0.12. The relationship between Heart Rate Reserve and the slope of the line can be determined with the following equation:
Advanced Compensated MET Formula:
Wt(kg) .25+(%HRR* .12) 4.22This formula will adjust the metabolic data to the body dimensions of any subject to a referenced standard, incorporating the use of % Heart Rate Reserve into the computation.
Although we have not completely satisfied the second requirement of a mathematically simple equation, the Simplified Compensated MET formula can still provide a high degree of accuracy in predicting maximum oxygen uptake and relative strength and power measurements. The Advanced Compensated MET formula, although more difficult to compute, can provide more reliable and accurate metabolic data across all %Heart Rate Reserve intensities.
Correcting Previous Data
The Compensated MET formulas that have been proposed have satisfied the requirement for a standardized method of assessment oxygen uptake and metabolism, and can provide a relatively simple mathematical process in the utilization of the formula. We must now concern ourselves with the ability to make the equation correct existing data.
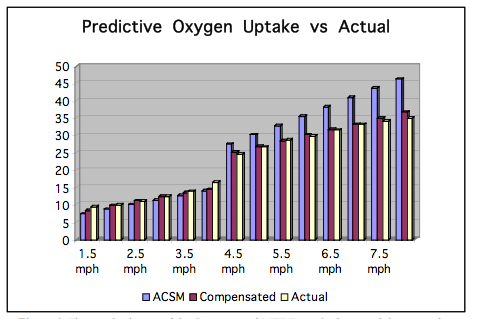
To show the accuracy of the Compensated MET formula, actual oxygen uptake in ml/kg * min-1 will be measured utilizing respiratory gas analysis on a treadmill protocol. The actual oxygen uptake scores will then be compared with the equations of the American College of Sports Medicine (1975), and a correction factor derived from the advanced Compensated MET Formula. A subject with a mass of 114 kg completed a treadmill protocol starting at 1.5 mph and was progressed .5 mph every two minutes. At 4.0 mph the subject was instructed to jog, thereby using both the walking and running formulas from the ACSM. The ACSM predictive formulas and the advanced Compensated MET Formula’s correction factor, were statistically compared to actual oxygen uptake measurements. Standard error for the predictive equations indicated that the Compensated MET Formula was associated with a standard error of .74, and the ACSM equations at 1.50. T-test of the ACSM’s equation failed to gain significance, (sig. p >.95), but reached significance in the Compensated MET formula, (p=.52 vs p=.95 respectively). The Compensated MET Formula had less than half of the standard error, and a significantly high level of confidence in the equations ability to predict oxygen uptake as opposed to the ACSM predictive equations for this subject, (Figure 4).
Figure 4: The standard error of the Compensated MET Formula decreased the error of prediction by over 50%, (Std Error: 1.50 vs 0.74), and gained statistical significance, (p=.95) when compared to the ACSM’s predictive equations for a 114 kg subject.
By multiplying by our conversion factor, (the reciprocal in this case) times the ACSM’s predictive equations, we have in essence accounted for over half of the standard error and gained a significantly superior equation in the prediction of oxygen uptake and made old data good. We have strong evidence to satisfy our third requirement for a method to make good the previous research obtained using traditional relative linear models for measuring oxygen uptake.
To summarize the information provided thus far:
- The method of measuring oxygen uptake has been made, utilizing a correction factor that can take into account differences in body dimension.
- The correction factor (termed the Compensated MET Formula) involves a relatively simple computation, that is not mathematically unwieldy.
- The use of the Compensated MET Formula can take existing methods of measurement, and through the use of a correction factor, attain significantly higher levels of accuracy in their estimation of oxygen uptake.
Prediction of Caloric Needs and Energy Metabolism
It is well known that oxygen consumption is dependent on foodstuffs metabolized. Carbohydrates are more efficient than fats, in terms of the oxygen it takes to produce a calorie of work. Computing the protein contribution is extremely complex with the various amino acids be broken down by a number of metabolic pathways. Lusk (1928) took on the daunting task of calculating the caloric yield of non-protein Respiratory Quotients, (now commonly referred to as Respiratory Exchange Ratios). By examining a table of ratios of carbon dioxide produced by the oxygen consumed, non- protein R values are given with the calories that are produced (Table 2).
Table 2: Non-protein R values derived by Lusk (1928). RER’s associated with the exclusive use of fats are = .707, carbohydrates are = 1.00. An RER = .85, or halfway between .707 and 1.00 would indicate the use of half fats and half carbohydrates.
With the information in Table 2, we can estimate calories based on % Heart Rate Reserve. It is well known that beyond the anaerobic threshold, carbohydrates are the predominant energy substrate, burning 5.047 calories per liter of oxygen consumed. At heart rates well below the anaerobic threshold, the body burns a percentage of calories from fats and ramps up the use of carbohydrates as the intensity increases. Naturally, there is a wide range of variables that can account for differences in what the body burns for energy at lower intensities. In general terms, it would be acceptable to assume a RER of .85 in well fed healthy subject at rest, with a ramping of RER to 1.00 at the anaerobic threshold, (can be estimated at 80% of heart rate reserve for an active healthy adult). A simple equation is provided to estimate the calories consumed at % Heart Rate Reserve under 80% (over 80% of Heart Rate Reserve uses 5.047 calories per liter).
%HRR Calorie Equation: 4.862+(%HHR*.231) = Kcal per liter of oxygen
With the information given thus far, we can accurately estimate with confidence the calories consumed during exercise metabolism.
- Determine the subjects oxygen uptake utilizing traditional methods.
- Multiply the resulting oxygen uptake by the correction factor obtained from the Compensated MET Formula.
- Multiply the Compensated oxygen consumption by the caloric yield per liter of oxygen consumed using the % Heart Rate Reserve Calorie Equation.
Applications of the Compensated MET Formula
It is apparent that the correction factor derived from the Compensated MET Formula, will greatly increase the accuracy of traditional methods of measuring oxygen uptake and metabolism. More importantly a standardized process has been proposed for a future of higher quality research, which allows direct comparisons of data between studies. Due to the increased accuracy of accounting for body dimensions in predicting metabolism, applications include:
A. Correction of dietary caloric predictions. We may need to re-evaluate overweight individuals that are diagnosed with a hypoactive thyroid using indirect calorimetry. An overweight patient of 150 kg would be estimated to have a daily caloric consumption of 3676 kcal. This patient, if measured with indirect calorimetry, would consume only 2917 kcal and be mistakenly diagnosed as with a 26% reduction in metabolic rate and prescribed medications needlessly.
B. A Fair Method of Performing Pre-employment Physical Assessments . Many pre-employment physical assessments assign a minimum level of oxygen uptake in METs or in ml/kg*min-1 for passing score. Because of the effect of body dimensions, a 150 kg candidate would have to have a 26% higher fitness level to get the same score of a 75 kg candidate applying for the same position. This would also jeopardize strength assessments that require of percent of body weight to be lifted during the examination.
C. Greater Accuracy in the Estimation of Fitness, Based on Exercise Tests. Physicians performing exercise testing without the benefit of respiratory gas analysis may greatly underestimate the fitness and exercise capacity of larger patients, and overestimate the fitness and oxygen consumption of smaller patients. When prescribing exercise, smaller subjects will be at increased risk of over training, and larger subjects may be under trained.
D. Increased Accuracy in Dosing Patients with Certain Medications. Many medications are prescribed in relation to metabolic rate. Smaller patients may be under prescribed and larger subjects over prescribed medications. By knowing the weight of the subjects in the medical studies conducted to determine proper dosing, a much more accurate method of prescribing medications can be provided. This could prove valuable in such medications are chemotherapy drugs that are often given on a per weight basis, where smaller subjects may be under prescribed medications that could save their lives.
E. Ability to conduct New Research Utilizing Increased Levels of Precision. Increased accuracy of predicting oxygen uptake may lead to a superior improvement in the quality of research on such topics as re-hydration. The Compensated MET Formula has been used successfully in the Eon series of Sport watches that can measure fluid loss with an increased accuracy as compared to overly simplified recommendation of the past.
It is apparent the application of this Compensated MET Formula can be far reaching and provide accuracy that has not been readily available until this time.
Research of the Past, Present and Future
VonDobln, Astrand & Bergstrom (1966) were early pioneers in research on body dimensions, acknowledged Brody’s (1945) contribution in predicting oxygen uptake. VonDobeln published a comprehensive review of factors related to oxygen uptake, and found ‘In this group, measurement of body size did not contribute to the prediction of max VO2.(p. 937). It was interesting that the 84 subjects of the study averaged 76.3 kilos (Std. Dev. =7.66 kg), similar to the dimensions of our reference human. The homogeneity of the study population may have been the reason for not seeing the impact of body dimension on the prediction of maximum oxygen uptake. Much of the advancing exercise physiology research on body dimensions and the effect on oxygen consumption may have been stalled with the well-publicized results of Von Dobeln’s study.
Currently, the number one priority for the exercise physiology community is to get the message out of the effect of body dimensions on oxygen uptake and metabolism. Peer review and quality research using the Compensated MET Formula will provide the exercise physiology community with access to a higher level of confidence in the collection of metabolic and exercise related data.
Research needs to be done on the effect of body composition on predicting metabolism, the variations of younger children that possess smaller, immature body dimensions, and the collection and collation of more accurate research to establish standards for physical fitness.
Conclusion
The ability to impact the way oxygen uptake and exercise metabolism is performed in exercise physiology today is a massive endeavor. We are witnessing the tip of the iceberg on new and exciting methods of determining oxygen uptake and metabolism. As professionals in the field of exercise physiology we need to ethically consider the ramifications of allowing the current methods of estimating oxygen consumption and metabolism to continue in their current state.
References
Astrand, P.O., & Rodahl, D. (1977) Textbook of work physiology: Physiological bases of exercise. New York: McGraw-Hill.
American College of Sports Medicine, (1983) The Recommended Quantity and Quality of Exercise for Developing and Maintaining Fitness in Healthy Adults. Med Science Sports Exercise, 15(IX-XIII).
American College of Sports Medicine,(1986) Guidelines for Exercise Testing and Prescription, 3rd Ed. Philadelphia: Lea & Febiger.
American College of Sports Medicine,(1991) Guidelines for Exercise Testing andPrescription, 4rd Ed. Philadelphia: Lea & Febiger.
Brody, S. (1945) Bioenergetics and Growth. New York: Reinhold Book Corporation.
Burke, E.R. (1998) Precision heart rate training. Champaign: Human Kinetics, pp 32-33.
Dobeln, W., Astrand, I. & Bergstrom, A. (1967) An analysis of age and other factorsrelated to maximal oxygen uptake. Journal of Applied Physiology. 22(5), 934-938.
Fox III, S.M. Naughton, J.P. & Haskell, W.L. (1971) Physical activity and the prevention of coronary heart disease. Ann Clin Res, 3, 404-432.
Hill, A.V. (1950) The dimensions of animals and their muscular dynamics. ScienceProgress. 38: 209-230.
Hemmingsen, A. (1960) Energy metabolism as related to body size and respiratory surfaces, and its evolution. Coppenhagen: C. Hamburgers.
Inbar, O. Oten, A. Scheinowitz, M. Rotstein, A. Dlin, R. & Casaburi, R. (1994) Normalcardiopulmonary responses during incremental exercise in 20-70-yr-old men. Med Sci Sport Exerc. 26(5), 538-546.
International Weightlifting Federation Website. Available: http://www.iwf.net. [July 10,2003].
Karvonen, M.J. Kentala, E. & Mustala, O. (1957) The effects of training on heart rate: a longitudinal study. Ann Med Exper Fenn. 35(3): 307-315.
Kleiber, M. (1932) Body size and metabolism. Hilgardia. 6, 315-353.
Lietzke, M.H. (1956) Relation between weightlifting total and body weight. Science. 124, 486-487.
Lusk, G. (1923) Science of nutrition, 4th Ed. Philadelphia: W.B. Saunders, p.65.
Massey, K. (2001, June 26). E-mail Correspondence, RE: Congestive Heart Failure Study. KennethMassey@pfizer.com.
Mathews, D.K., & Fox, E.L. (1976) The Physiological Basis of Physical Education and Athletics, 2nd Ed. Philadelphia: W.B. Saunders.
McMahon, T.A., & Bonner, J.T. (1983) On size and life. New York: W.H. Freeman.
O’Shea, J.P. (1976) Scientific Principles and Methods of Strength Fitness, 2nd Ed. Reading, MA: Addison-Wesley.
Robergs, R.A. & Landwehr, R. (2002) The surprising history of the ‘HRmax = 220-age equation. Journal of Exercise Physiology Online, 5(2), May 2002.
Ross, R. M. (1989) Interpreting Exercise Tests. Houston: CSI Software.
Rubner, M. (1883) Ueber den Einfluss der Korpergroesse and Stoff- und Kraftwechsel. Z. Biol. Munich. 19, 535-562.
Sensormedics (1991) Vmax Computer Software Manual, Version 0101-05-2C, Equation 229.
Surina, B.J. (2003) Universal Skinfold Equation for the Estimation of Body Fat. Unpublished.
Tanka, H. Monohan, K.G. & Seals, D.S. (2001) Age “ predicted maximal heart rate revisited. J Am Coll Cardiol. 37:153-156.
Vaage, O. & Hermansen, L. (1977) Maximal Oxygen Uptake in a group of Norwegian top athletes trained in different events. From Astrand, P.O., & Rodahl, D. (1977) p 377.