Optimal Individualized Sweat Loss and Fluid Replacement Rate via Temperature, Humidity, Heart Rate and Metabolic Indices.
ABSTRACT: Hydration research concluded by the Exercise Science Center tested 10 firefighters in extreme environmental conditions and found a high correlation between actual fluid loss on the scale versus fluid loss determined by mathematical algorithms, (r=.917). Variables included in the determination of accurate fluid loss include proprietary algorithms for adjustments in body dimensions, heart rate algorithm as they relate to maximal oxygen consumption (Max VO2), adjustments for foodstuffs metabolized at various exercise intensities, metabolic adjustments for aging, and environmental sensor inputs for time, temperature and humidity. Individualized optimal fluid loss and replacement rates can be displayed in an electronic device (Acumen Inc. Patent No. US6138079), Drink alarms allow optimal performance to continue in hostile environments, thereby avoiding injuries related to dehydration, hyperhydration, and hyponatemia. With minimal individual input of resting heart rate, maximal oxygen consumption (VO2 max based on 2 mile time) and the body weight, accurate estimation of fluid loss and rate of fluid replacement can be made.
Introduction
Fluid loss has typically been approximated using linear regression equations correlating the losses recorded during some bout of activity with any number of monitored physiological variables, (post hoc). A more novel approach is to apply basic physiological principles involved in fluid loss and see how well they can forecast actual fluid losses, (hypothesize).
One of the biggest challenges was to simplify the complexity of the physiological variables involved in the calculation, most important of these is the determination of calories burned. If this could be done, then algorithms could be built into an interactive heart rate and environmental sensors in a watch type device to accurately determine fluid loss.
Effect of Body Dimension
Determining calories involves many factors involved in the accurate estimation of aerobic power that are often overlooked Most information derived from the measurement of oxygen uptake during exercise is collected using indirect calorimetry. Investigators generally recognize resting oxygen uptake as equal to 3.5 ml of oxygen consumed per kilogram per minute (ml/kg*min –1). By measuring oxygen uptake in ml/kg*min –1 during activity, investigators believed that they could determine the oxygen needed to perform various activities. The beauty of the model was that different sized individuals would likely require the same relative oxygen uptake on a per weight basis. Consequently, the larger individual would be able to perform twice the absolute work at the same relative oxygen uptake.
Traditional Linear Model of Measuring Relative Aerobic Power
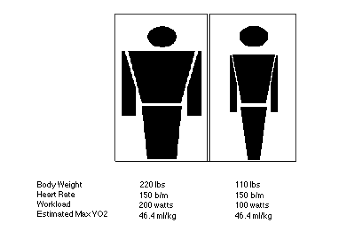
Figure 2: Traditional methods of assessing relative oxygen uptake propose that a subject of twice the mass would need to do twice the work to get the same score for aerobic power.
Subject’s of twice the weight do not posses twice the blood volume, or lung capacity, etc… of a person half their body weight. VonDobeln, Astrand & Bergstrom (1966) were early pioneers in research on body dimensions and the effect on the measurement of oxygen uptake. VonDobeln published a comprehensive review of factors related to oxygen uptake, and found measurement of body size did not contribute to the prediction of max VO2. It was interesting to note the homogenous nature of the study population, averaging 76.3 kg, (SD= 7.66 kg). It is quite possible the lack of a diverse study population in terms of mass may have stalled future physiological research on body dimensions and the effect on oxygen uptake.
Body Dimension and Hydration Study
Twenty subjects, representing a physiological diverse sample of regular exercisers at an exercise facility, were recruited for a dehydration study. Each subject was weighed nude both before and after a two hour exercise bout on a motor driven treadmill at 4 mph and a 1% grade.
Actual fluid loss was obtained as a difference between the pre and post weights of the subjects with exercise. Actual fluid loss was correlated with the predictive equation copyrighted by Fluid Check, and two other equations, which are commonly used to predict fluid loss, (Ashrea and Nieman equations). The Fluid Check system has the added benefit of accounting for varying environmental conditions associated with humidity and temperature. For the purposes of this study it should be noted that the environmental conditions (60-65 degrees, 50-60% humidity) were conducive to all three equations.
Sample Population
Purposive sampling of subjects were selected to achieve a diversity of sexes, ages, weights and heights, % body fats, and BMI’s, (10 males, 10 females). All subjects were active and were capable of completing the prescribed exercise intensity and duration, (4 mph, 1% grade, 2 hours).
Actual losses were measured as the difference between the pre and post weights associated with the exercise session. The subjects were then asked at the conclusion of the exercise session how much water they would typically drink on their own volition after similar exercise, and given a sixteen ounce bottle of water to use as a reference.
Statistical Procedure
The Pearson r coefficient correlation statisticwas utilized to compare the three equation used to predict fluid loss, with actual fluid losses in each of the study subjects. A Pearson r was also used to compare the subjects self reported fluid hydration amounts with actual fluid loss.
Study Results
Results showed that all three predictive equations showed a significant relationship with actual fluid loss. The Pearson r for the Fluid Check System, using compensations for body dimensions was the highest at .80, with the Ashrae and Nieman Equations at .78. Their was no significant correlation attributed with self reported hydration amounts and Actual fluid losses for the subjects tested, (r=.11). Mean losses recorded by the Fluid Check System was the only equation within one standard deviation of Actual mean losses.
The study suggested that the effect of compensating for body dimension was a significant factor in predicting oxygen consumption, calories burned and fluid loss. Since the data on body dimensions has a strong scientific foundation in physics, the next step was to supplement this information with a standardized system to more accurately estimate aerobic power.
Submaximal Exercise Testing to Predict Maximal Aerobic Power
A number of testing protocols that have attempted to estimate aerobic power based on the heart rate response to submaximal workloads. By extrapolating the slope of the heart rate/workload relationship to a maximal heart rate, maximal aerobic power can be estimated.
- Use the known maximal heart rates or maximal aerobic performance times if available, (2 mile run time). Utilize scientifically derived mode and population specific equations for the estimating maximum heart rate. Better equations are constantly being developed.
- To avoid confusion in the recommendations for exercise intensity, utilize the percent of Heart Rate Reserve method which has a more direct relationship to percent of Max VO2.
- If extrapolation of the Heart Rate/Workload relationship is the method employed to predict aerobic power, ensure a range from 40% to 80% of the Heart Rate Reserve is utilized.
Mass as it Relates to Metabolic Rate
When in a resting state, the volume of the skeletal voluntary muscle mass is dormant, while the autonomic system, is always metabolically active. As exercise intensities increase, blood may be shunted away from the organs and smooth muscles into the more dynamic and active working muscles. The basal metabolic contribution to the total oxygen uptake is altered, thus reflecting a noted change seen in its relationship to body mass.Another factor involved in the limitation of peak exercise performance and oxygen uptake is the dissipation of heat. Thus during maximal aerobic exercise their may be less oxygen consumed and less work being done because of an inability to radiate heat as effectively in larger animals.
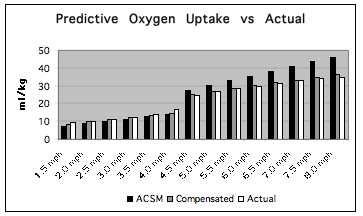
Figure 4: The standard error of the Compensated MET Formula decreased the error of prediction by over 50%, (Std Error: 1.50 vs 0.74), and gained statistical significance, (p=.95) when compared to the ACSM’s predictive equations for a 114 kg subject.
The generally accepted use of a relative resting MET of 3.5 ml/kg/min-1 for everyone makes no allowance for differences in body dimension in metabolic studies. This practice has no basis in fact, and can greatly affect the accuracy in which estimations of oxygen uptake are currently being made. Also the relationship between oxygen uptake and body mass does not appear to be a fixed relationship, but allometric, with changes in the relationship of mass to oxygen uptake depending on the intensity and mode of exercise. The construction of an allometric equation referred to as the Compensated MET formula, although more difficult to compute, can provide more reliable and accurate metabolic data across all % Heart Rate Reserve intensities and body dimensions.
Method
To show the accuracy of the Compensated MET formula, actual oxygen uptake in ml/kg * min-1 was measured utilizing respiratory gas analysis (MedGraphic Vmax System) on a treadmill protocol. The actual oxygen uptake scores will then be compared with the equations of the American College of Sports Medicine (1975), and a correction factor derived from the advanced Compensated MET Formula. A subject with a mass of 114 kg completed a treadmill protocol starting at 1.5 mph and was progressed .5 mph every two minutes. At 4.0 mph the subject was instructed to jog, thereby using both the walking and running formulas from the ACSM (1991). The ACSM predictive formulas and the advanced Compensated MET Formula’s correction factor, were statistically compared to actual oxygen uptake measurements.
Results
Standard error for the predictive equations indicated that the AdvancedCompensated MET Formula was associated with a standard error of .74, and the ACSM equations at 1.50. T-test of the ACSM’s equations to actual measurements failed to gain significance, but did in the Advanced Compensated MET formula, (p=.52 vs p=.95 respectively). The Advanced Compensated MET Formula had less than half of the standard error, and a significantly high level of confidence in the equations ability to predict oxygen uptake as opposed to the ACSM predictive equations for this subject, (Figure 4).
Prediction of Caloric Needs and Energy Metabolism
It is well known that beyond the anaerobic threshold, carbohydrates are the predominant energy substrate. At heart rates well below the anaerobic threshold, the body burns a higher percentage of calories from fats and ramps up the use of carbohydrates as the intensity increases. In general terms, the accuracy in the estimation of calories burned could be increased further, by relating exercise intensity to energy substrates utilized.
Extreme Environmental Conditions
A study was undergone to see how closely dehydration could be forecasted in extreme environmental conditions. Calorie adjustments for body dimensions and foodstuffs utilized as it relates to varying exercise heart rates, temperature and humidity was performed using a simplified algorithm
Methods:
Ten paid firefighters volunteered to participate in a study to measure fluid loss during fire fighting. Subjects were scheduled for a physical assessment to obtain physiological characteristics as well as to estimate their aerobic capacity. On the morning of the study, subjects were weighed nude prior and immediately after a practice burn of a residential structure. Subjects were also fitted with a heart rate monitor (Polar Vantage XL or the Acumen TZ Max 100). Temperature and humidity reading were taken at 15 to 30 minute intervals from the inside of the firefighter’s turnout gear using temperature and humidity sensors supplied by Acumen. Subjects were provided with a carbohydrate replacement drink, and the amount ingested and expelled throughout the test period was recorded and used in the computation of fluid loss during the study period.
Results:
Twelve subjects started the study, and ten completed the study. Two subjects experienced technical difficulties, (one subject damaged the watch, and the other inadvertently turned the watch off during the collection period).
Heart rates during the work interval were taken each minute and converted into percent of maximum heart rate using the heart rate reserve method (Karvonen). The recorded resting heart rate was determined, and estimated maximum heart rate was based on the equation of Tanaka at 207-(age * .70). Firefighters during the work interval ranged from 23.2 to 52.8% of estimated maximum heart rate, with a mean for the 10 firefighters of 37.6%.
Calculations of kilocalories burned were made based on the heart rate/workload data obtained from the firefighters laboratory assessed submaximal estimation of maximal oxygen consumption. Compensations for calories burned were made for body dimension. Subject work intervals ranged from 96 to 370 minutes, with an average time of 204 minutes. Total calories expended for the activity ranged from 373 kcal to 1731 kcal, with an average use of 974 kcal for the work performed during the study interval. Adjustments were also made for the estimated respiratory exchange ratios of the subjects during exercise, which utilized percent of maximum heart rate data.
The kilocalorie, temperature and humidity variables that were collected were used in the equation derived by the Fluid Check System. Estimated fluid loss during the task of fire fighting was computed for each of the ten test subjects. Actual fluid losses recorded for the fire fighters tested ranged from 20.0 ounces to 108.8 ounces of fluid loss with an average loss of 52.4 ounces lost. Fluid loss estimates ranged from 23.3 ounces to 122.3 ounces, with an average estimated loss of 67.0 ounces of fluid (Figure 3).
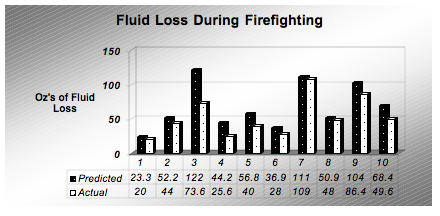
Figure 3: Predicted vs actual fluid loss during the task of fire fighting for 10 subjects.
A statistical analysis of the individual results demonstrated a high correlation (r= .917) between predicted and actual fluid loss values. Significance was to .01 level, (p = .008), with a standard error , SE= 4.33 ounces. Individual data showed that none of the subjects were under predicted, with a noted range of re-hydration was from 102.4% to 166%, with an average of 127.9% re-hydration rate.
Discussion:
The accurate prediction of fluid loss is related directly to the ability to accurately predict caloric expenditure. By utilizing simple field tests for the prediction of maximal oxygen consumption, compensating for body dimensions, accurate prediction of fluid loss can be realized. Variables needed to predict fluid loss in the study of the firefighters include the, resting heart rate, body weight, and estimated MET’s. Using obtained heart rates from a continuous heart rate monitor, with built in temperature and humidity sensors, prediction of fluid loss can be done across a variety of exercise intensities, durations and modalities.
Applications of the Compensated MET Formula
It is apparent that the correction factor derived from the Compensated MET Formula, will greatly increase the accuracy of traditional methods of measuring oxygen uptake and metabolism. More importantly a standardized process has been proposed for a future of higher quality research, which allows direct comparisons of data between studies. Due to a the increased accuracy of accounting for body dimensions in predicting metabolism, applications include:
A. Correction of dietary caloric predictions. An overweight patient of 150 kg would be traditionally estimated to have a daily caloric consumption of 3676 kcal. This patient, measured with indirect calorimetry, would consume only 2917 kcal and may be mistakenly diagnosed with a 26% reduction in metabolic rate and prescribed medications needlessly.
B. A Fair Method of Performing Pre-employment Physical Assessments . Many pre-employment physical assessments assign a minimum level of oxygen uptake in METs or in ml/kg*min-1 for passing score. Because of the effect of body dimensions, a 150 kg candidate would have to have a 26% higher fitness level to get the same score of a 75 kg candidate applying for the same position. This would apply to strength assessments requiring a percent of body weight to be lifted during the assessment, thus giving larger candidates a distinct disadvantage.
C. Greater Accuracy in the Estimation of Fitness, Based on Exercise Tests. Exercise testing without the benefit of respiratory gas analysis may greatly underestimate the fitness and exercise capacity of larger patients, and overestimate the fitness and oxygen consumption of smaller patients. When prescribing exercise, smaller subjects will be at increased risk of over training, and larger subjects may be under trained.
D. Increased Accuracy in Dosing Patients with Certain Medications. This could prove valuable for such medications as chemotherapy and malaria drugs that are often given on a per weight basis. Smaller patients may be under prescribed and larger subjects over prescribed medications. The use of the Compensated MET Formula could save lives by providing a more accurate method of dosing medications.
E. Ability to conduct New Research Utilizing Increased Levels of Precision. Increased accuracy of predicting oxygen uptake may lead to higher quality of research on such topics such as hydration, which may be directly linked to aerobic metabolism.
Conclusion
The ability to impact the way that estimations of aerobic power and exercise metabolism are measured in exercise physiology today is a massive endeavor. As professionals in the field of exercise physiology we need to incorporate the compensations of body dimensions to create a fair set of standards for individuals regardless of body dimensions. Future research should center on validation of equations and procedures currently being used in the estimation of aerobic metabolism. More research is needed in subjects with extreme body dimensions which include children, athletes, and the morbidly obese. By studying the mechanisms underlying the accurate estimates of exercise metabolism a greater understanding of the physiology of exercise can be realized.
References
Astrand, P.O., & Rodahl, D. (1977) Textbook of work physiology: Physiological bases of exercise. New York: McGraw-Hill.
American College of Sports Medicine, (1983) The Recommended Quantity and Quality of Exercise for Developing and Maintaining Fitness in Healthy Adults. Med Science Sports Exercise, 15(IX-XIII).
American College of Sports Medicine,(1986) Guidelines for Exercise Testing and Prescription, 3rd Ed. Philadelphia: Lea & Febiger.
American College of Sports Medicine,(1991) Guidelines for Exercise Testing and Prescription, 4rd Ed. Philadelphia: Lea & Febiger.
Brody, S. (1945) Bioenergetics and Growth. New York: Reinhold Book Corporation.
Burke, E.R. (1998) Precision heart rate training. Champaign: Human Kinetics, pp 32-33.
Dobeln, W., Astrand, I. & Bergstrom, A. (1967) An analysis of age and other factors related to maximal oxygen uptake. Journal of Applied Physiology. 22(5): 934-938.
Fox III, S.M. Naughton, J.P. & Haskell, W.L. (1971) Physical activity and the prevention of coronary heart disease. Ann Clin Res, 3, 404-432.
Hill, A.V. (1950) The dimensions of animals and their muscular dynamics. Science Progress. 38: 209-230.
Hemmingsen, A. (1960) Energy metabolism as related to body size and respiratory surfaces, and its evolution. Coppenhagen:
C. Hamburgers, Inbar, O. Oten, A. Scheinowitz, M. Rotstein, A. Dlin, R. & Casaburi, R. (1994) Normal cardiopulmonary responses during incremental exercise in 20-70-yr-old men. Med Sci Sport Exerc. 26(5): 538-546.
International Weightlifting Federation Website. Available: http://www.iwf.net. [July 10, 2003].
Karvonen, M.J. Kentala, E. & Mustala, O. (1957) The effects of training on heart rate: a longitudinal study. Ann Med Exper Fenn. 35(3): 307-315.
Kleiber, M. (1932) Body size and metabolism. Hilgardia. 6, 315-353.
Lietzke, M.H. (1956) Relation between weightlifting total and body weight. Science. 124, 486-487.
Lusk, G. (1923) Science of nutrition, 4th Ed. Philadelphia: W.B. Saunders, p.65.
Massey, K. (2001, June 26). E-mail Correspondence, RE: Congestive Heart Failure Study. KennethMassey@pfizer.com.
Mathews, D.K., & Fox, E.L. (1976) The Physiological Basis of Physical Education and Athletics, 2nd Ed. Philadelphia: W.B. Saunders.
McMahon, T.A., & Bonner, J.T. (1983) On size and life. New York: W.H. Freeman.
McArdle, W.D. Katch, F.I. & Katch, V.L. (1981) Exercise physiology: Energy, nutrition and human performance. Philidephia: Lea&Febiger.
O’Shea, J.P. (1976) Scientific Principles and Methods of Strength Fitness, 2nd Ed. Reading, MA: Addison-Wesley.
Robergs, R.A. & Landwehr, R. (2002) The surprising history of the “HRmax = 220- age” equation. Journal of Exercise Physiology Online, 5(2), May 2002.
Ross, R. M. (1989) Interpreting Exercise Tests. Houston: CSI Software.
Rubner, M. (1883) Ueber den Einfluss der Korpergroesse and Stoff- und Kraftwechsel. Z. Biol. Munich. 19, 535-562.
Sensormedics (1991) Vmax Computer Software Manual, Version 0101-05-2C, Equation 229.
Swain, D.P. Abernathy, K.S. Smith, C.S. Lee, S.J. & Bunn, S.A. (1994) Target heart rates for the development of cardiorespiratory fitness. Med.Sci. Sports Exerc. 26(1):112-116.
Surina, B.J. (2003) Universal Skinfold Equation for the Estimation of Body Fat. Unpublished.
Tanaka, H. Monohan, K.G. & Seals, D.S. (2001) Age – predicted maximal heart rate revisited. J Am Coll Cardiol. 37:153-156.
Vaage, O. & Hermansen, L. (1977) Maximal Oxygen Uptake in a group of Norwegian top athletes trained in different events. From Astrand, P.O., & Rodahl, D. (1977) p 377.
| |
